A prime number is defined as a natural number greater than 1 with no positive divisors other than 1 and itself. How would you answer if anyone asked you, “What are all prime numbers less than 10.000?” We will answer this question in a pretty cool way.

There are a plethora of algorithms for locating all prime numbers up to a certain limit. In this post, I’ll go through the Eratosthenes Sieve, a simple but effective algorithm. In fact it is a really old algorithm developed by Eratosthenes of Cyrene. He is best known for being the first person to calculate the circumference of earth.

Sieve of Eratosthenes

To find all the prime numbers less than or equal to a given integer n by Eratosthenes’ method:

1. Create a list of consecutive integers from \(2\) through \(n\). So basically \((2,3,4,5,6,...,n)\).

2. Initialize \(p= 2\) after the definiton of prime numbers as the smallest prime number in the list.

3. Enumerate the multiples of \(p\) by counting to \(n\) from \(p^2\) in increments of \(p\). Furthermore mark them in the list. (these will be \(p^2,p^2+p,2p,...\), p should not be marked)

4. Find the first number greater tha \(p\) in the list that is not marked. Set \(p\) now equal to this specific number (which is the next prime), and repeat from step 3. If \(p^2 >n\), stop.

5. When the algorithm terminates, the numbers remaining not marked in the list are all the primes number not greater than \(n\)

This process is visualised in the following GIF:

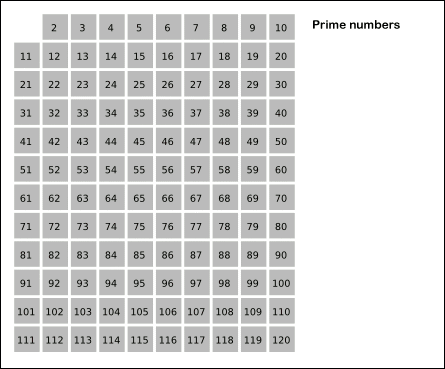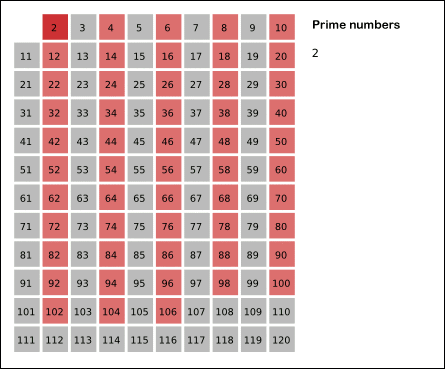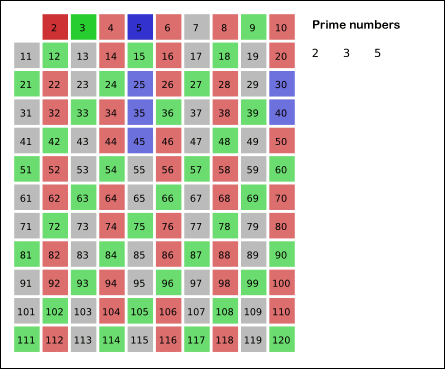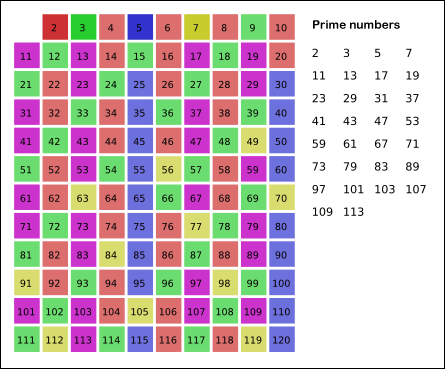
Implementation

R Code

sieve <- function(n) {
  # Vector, everthing set to TRUE
  prime <- rep(TRUE, n)  
  # Removed one from output (by Definition)
  prime[1] <- FALSE  
  
  # Mark FALSE if composite index.
  for (i in 2:sqrt(n)) {
    if (prime[i]) prime[seq(i ^ 2, n, i)] <- FALSE
  }
  # Return only TRUE indices 
  which(prime)  
}

# Example, find all prime numbers less or equal to 10
sieve(10)

## [1] 2 3 5 7

Python Code

def SieveOfEratosthenes(n):
	
	# Create a boolean array "prime[0..n]"
	# all entries are initialized as true. A value in prime[i] will
	# finally be false if i is Not a prime, else true.
	prime = [True for i in range(n + 1)]
	p = 2
	while (p * p <= n):
		
		# If prime[p] is not changed, then it is a prime
		if (prime[p] == True):
			
			# Update all multiples of p
			for i in range(p * 2, n + 1, p):
				prime[i] = False
		p += 1
	prime[0]= False
	prime[1]= False
	# Print all prime numbers
	for p in range(n + 1):
		if prime[p]:
			print(p) 

n= 10
SieveOfEratosthenes(n)

## 2
## 3
## 5
## 7

Shiny App to answer our question

Thougths

I learned this algorithm in my university course “Algorithms and Data Structures” and it caught my interest immediately. It was a lot of fun tom implement this algorithm in R and Python. However, in my opinion Python fits better for this specific purpose.